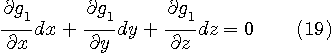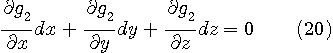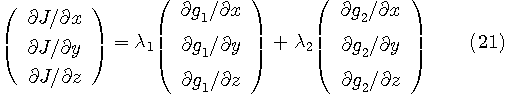|
変分法 Calculus of variation |
|
関数のスカラー関数を汎関数 (Functional ) と呼んでいますが、この極大と極小を与えられた拘束条件のもとで求める問題は、物理学などで古くから研究されてきました。 変分法は、このような問題を統一的に解く数学的手法です。 いきなり関数空間を考えるのは直感的理解が困難なので、まずは変数(ベクトル空間)のスカラー関数について、変分法の原理を直感的に説明します。 汎関数への拡張は、その原理をそのまま関数空間にもち込むことになりますが、関数空間の数学的体系は専門書を読んでください。 次のような例題を解いてみましょう。
誰もが考える方法は、
から、
のような形を求め、これを
に代入して、変数
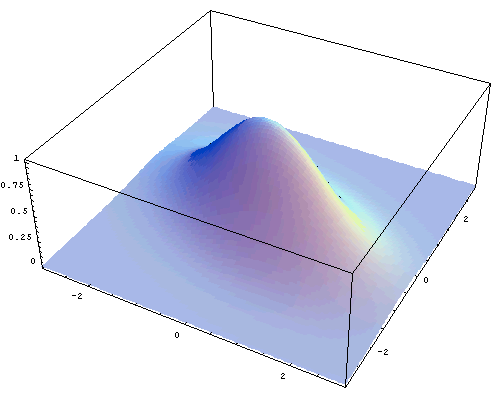
として、この問題の様子を図解してみます。 曲面
そして、上の曲面を
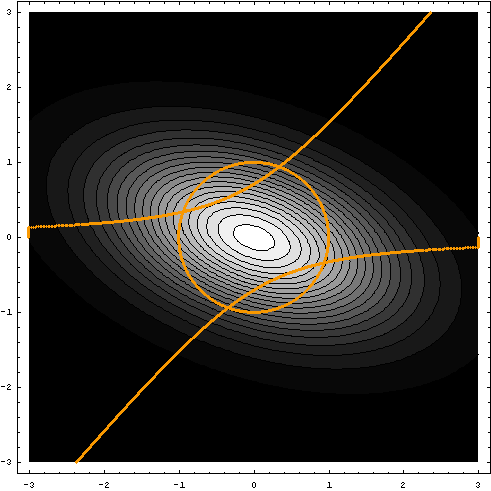
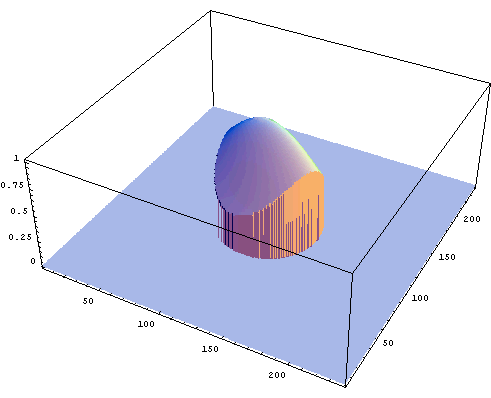
で切り取ってみましょう。 すると問題は次のように言うことができます。 上から見ると円形をした島があり、この崖のふちに沿って道がある。
極小点または極大点では、道に沿った接線と曲面
になっていなければなりません。 もし、両方の接線が交叉していると、そこは極小あるいは極大になっていません。 逆に言えば、上のことが成り立つ地点は極大または極小(厳密に言えば、鞍点も含む。 これらを総称して停留点と呼ぶ)になっています。 「接線が同じ」という数学的表現は次のようになります。 まず、
ですが、接線方向の変分は
が等高線の接線(あるいは法線)を与えています。 ちなみに、
が接線の勾配を表しています。 一方、拘束条件の接線は、
を満たします( 式(6)と(8)の
であり、ちょっと書き換えて、
です。 式(10)の値を
が得られ、式(11)と拘束条件(1)を連立させれば、停留点を求めることができます。 このことは、
の極値を求めることと同等です。 以上が、ラグランジェ (Joseph Louis Lagrange, 1736-1813) の未定乗数法です。 では、式(12)を用いて、冒頭の例題を解いてみましょう。 極値が満たす式は次の3つです。
の解で極値をとり、
次に、この方法を3次元に拡張し、拘束条件を二つにしてみます。
それぞれの拘束条件は点 停留点では、 ということになります。 このことは、
が、二つの接面、
に従属していることを意味しているので、
が成り立っていなければなりません。 したがって、
の極値を求める問題に帰着します。 多次元の一般原理は、この考察をストレートに拡張すれば得られます。 汎関数の場合、解が連続関数として求まるならば、ラグランジェの未定乗数法を適用することができます。 たとえば、よく遭遇する下記のような問題を想定してみます。
コンピューターによる直接的な数値計算法は、x 軸をサンプリングして、多次元のラグランジェの未定乗数法を適用して得られます。 最初に変分法を考え出したオイラー ( Leonhard Euler 1707-1783) もこのような道筋で考えました。 実際、サンプリング間隔を十分細かくしたとき、少し隔たった区間では、変分が独立なので、次のような状況に帰着します。 汎関数
において、関数
したがって、
を代入し、
が任意の |
 の等高線の接線が同じ
の等高線の接線が同じ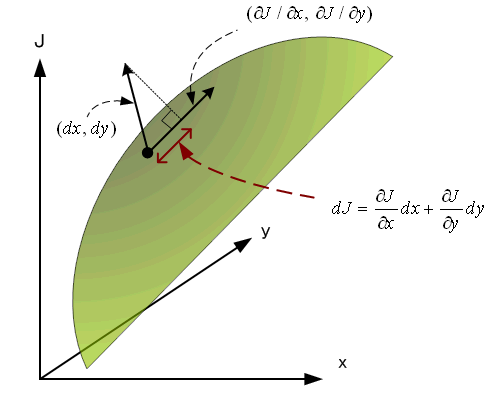
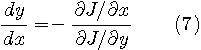
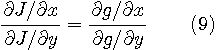
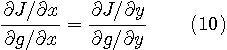
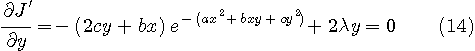
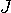 の等高線の接線が同じになっていることが読み取れます。
の等高線の接線が同じになっていることが読み取れます。