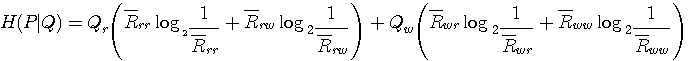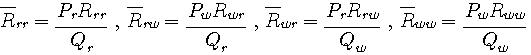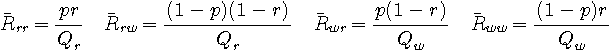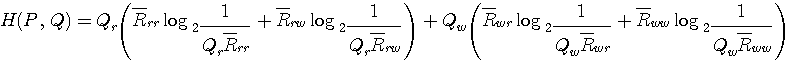|
相互情報量 Mutual information |
|
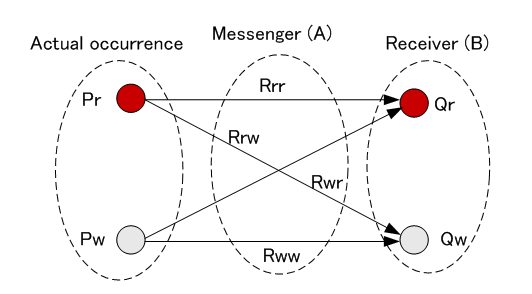
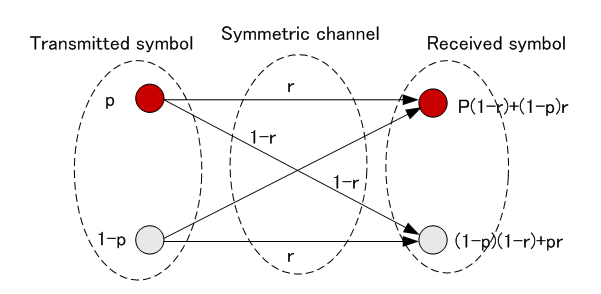
伝言ゲーム 赤っぽい色をした物と白っぽい色をした物がランダムに現れるとします。 前者の頻度を Pr、後者の頻度を Pw とします。 これを見たA君が、赤か白かをB君に伝えます。 A君が赤を正しく伝える確率を Rrr、赤を白に間違って伝える確率を Rrw、白を正しく伝える確率を Rww、白を赤に誤って伝える確率をRwr とします。 B君はA君の伝言を聞いたとき、平均として本当の色についてどれだけの情報を得るでしょうか? これに答えるのが相互情報量という尺度です。
Pr + Pw = 1 Rrr + Rrw = 1 Rww + Rwr = 1 Qr = PrRrr + PwRwr (B君が赤を聞く確率) Qw = PrRrw + PwRww (B君が白を聞く確率) 伝言ゲームは通信のモデルそのものです。 送信された情報は、チャンネルを通過する間に雑音や波形歪みを受け、ときどき誤って受信されます。 チャンネルがA君、受信機がB君に相当します。 上の伝言ゲームで Rrr=Rrw=Rwr=Rww=1/2 は、A君がまったくいいかげんに伝えていることを意味しています 。通信で言えば、チャンネルでものすごく大きな雑音が加わり、受信機は送信情報をなにも受けていない状態に相当します。 逆に、Rrw=Rwr=0 ならば、A君の伝言がいつも正しいことを意味し、チャンネルでは歪も雑音もなく、正確に情報が受信されていることを表しています。 この伝言ゲームをもっと正確に分析することから、通信の基本的概念を導くことができます。 そして、その概念から多くの実用的な原理が導かれます。 この伝言ゲームで登場する各種の確率について形式的なエントロピー(それが平均としてどれだけの情報を運んでいるかという尺度)を定義し、その物理的な意味を考えてみましょう。 注1 : その前にエントロピーの概念を理解しておく必要があります。 ちょっとこの概念の難しさについて触れておきます。 エントロピーとは情報のあいまいさ、すなわち規則性からの隔たりを測る尺度です。 対象とする情報源のエントロピーが小さいとき、それが出力する情報のあいまいさは小さく、規則性が大きいことを意味しています。 このとき、ぼく達はその情報源からあんまり多くの情報量を期待できないことを示唆しています。 これは、あくまでも平均的な意味においてです。 ちょうど、いつも同じことばっかり言っている人から平均として多くの情報が引き出せないといっているわけですが、はたして本当でしょうか? もしも彼が嘘をついたら、ものすごく大きな情報を得ますね。 もう少し具体的な例を挙げてみましょう。 同じ数の赤球と白球がいっぱい入った袋からランダムに10個の玉を取り出して一列に並べてみます。 この系列のパターンは全部で 1024 通りあり、どれも同じ確率で出現します。 したがって、並べられたパターンを見たときに得る情報はどれも同じと考えるのが自然であり、このときのエントロピーは容易に計算できます。 次に、赤球が10個、白球が10000個入った袋からランダムに10個の球を取り出して一列に並べてみましょう。 すると、並べられたパターンは圧倒的に白が多いでしょう。 ましてや、すべて赤になるケースは何回やっても実現しないぐらい起こりにくいことです。 白が多いパターンを見たときに得る情報は小さいが、赤が多いパターンを見たとき得る情報はものすごく大きいですね。 それでは、前者と後者のケースを比較して、情報量の期待値はどちらが大きいと考えるべきでしょうか? この答えは、情報量をどのように計量化するかに依存します。 シャノンは情報量を対数で定義しましたが、この場合のエントロピーはどうなるでしょうか? もう一度、情報を測ると平均情報量(エントロピー)を参照してください。 では、冒頭の伝言ゲームについて、いろんなエントロピーとその物理的意味を列挙します。 相互情報量は最後に登場します。以下、図解の簡単のため、 伝言者Aが、赤を白に、白を赤に間違うのは同じ(対称チャンネル) とします。 [1] 情報源のエントロピー
これは、実際に生起する赤と白の系列がどれだけランダムかを表します。 言い換えれば、送信情報源が平均としてどれだけの情報量を出しているかを表しています。 この概念をエントロピーと呼んでいます。
[2] 伝言結果のエントロピー
B君が一回の伝言を聞いたとき、平均として得る情報量です。 ここで、
ですが、対称チャンネルなので、
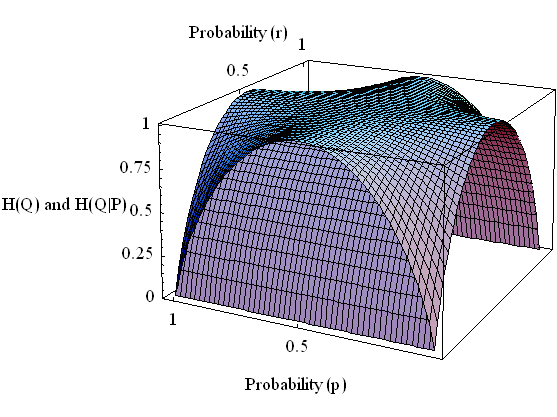
[3] 伝言者のエントロピー
右辺の最初のカッコ内は赤であることを知った後での伝言結果のエントロピーを、2番目のカッコ内は白であることを知った後での伝言結果のエントロピーを表しています。 そして右辺全体は、それぞれを赤と白の生起確率で平均した形をしています。 左辺の記号において、タテ棒の右側は条件、左側はその条件のもとでの伝言結果を表していますから、実際の赤白が分かった時点で(実際の赤白の系列に関する情報量は除いてしまって)、伝言者A君が新たにどの程度のあいまいさを作り出すかを表しています。 A君があいまいでない、すなわち伝言がいつも正確なときは、
ですが、このとき
ですが、このとき
となります。非対称チャンネルのときは
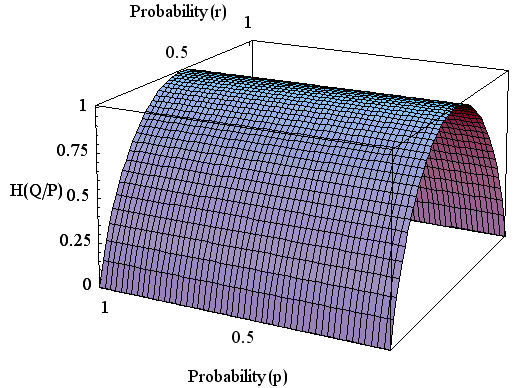
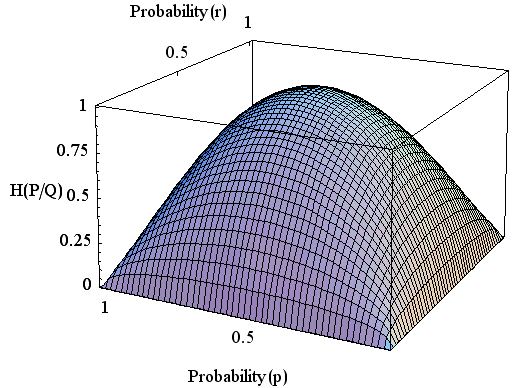
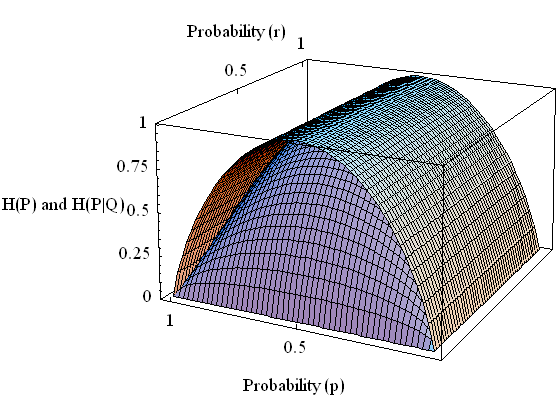
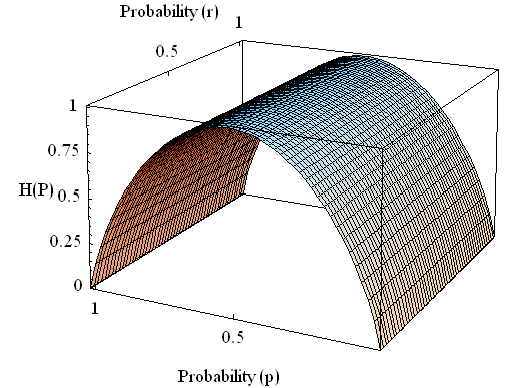
[4] 伝言結果を知った後の情報源のエントロピー
で与えられます。 左辺のタテ棒の右側には受信者、左側には送信者が配置されています。 すなわち、受信結果が分かった時点で、なお送信情報に残されるあいまいさを表しています。 同じく、対称チャンネルとします。
この曲面を描いてみましょう。 伝言者A君がいつも正しい( r = 0 )場合、伝言者がかならず逆をいう場合( r = 1 )、赤しかでない場合( p = 1 )、白しか出ない場合( p = 0 )、これらのいずれかにおいては、伝言結果には不確定さが残らないことが読み取れます。
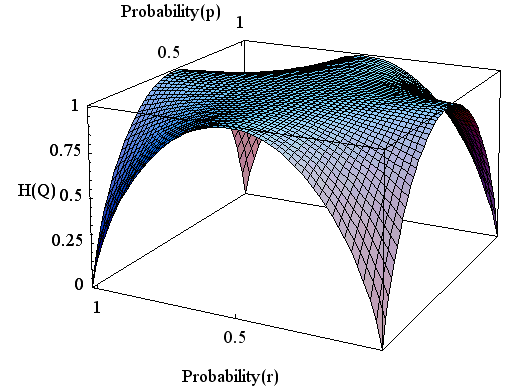
[5] 情報源と伝言結果の同時エントロピー(2次元)
たとえば、
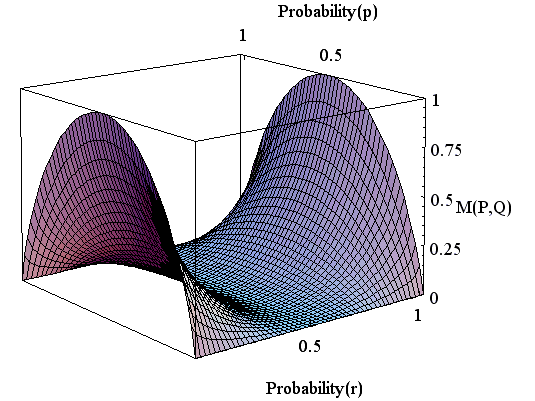
やはり、対称チャンネルを仮定して曲面を描いてみましょう。 縦軸の最大が2になっていることに注意してください。
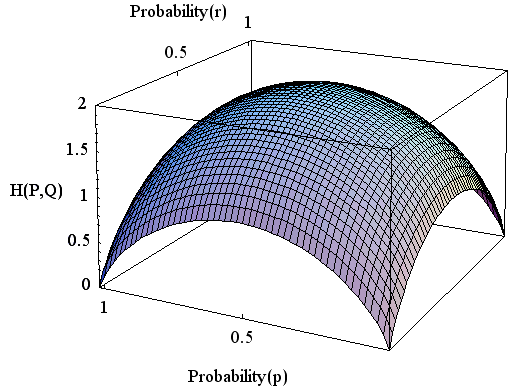
以上、合計5つのエントロピーを挙げましたが、少し辛抱強く計算すれば、次のような公式が成り立っていることがわかります。
これを相互情報量 (mutual information) と呼んでいます。 計算は直感的でないので、注3 の図を見ながら、その意味をつかんでください。 関係式を列挙すると次のようです。
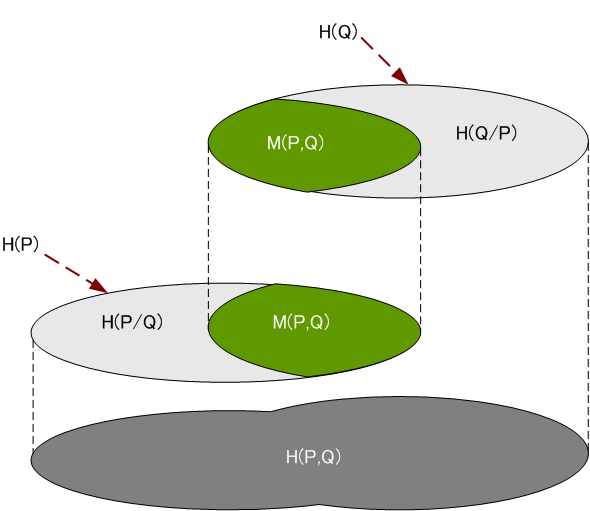
これらから、各エントロピーの関係を下のように描くことができます。 注2:下図では、
緑色で塗りつぶされた部分が相互情報量
注3:上の相互情報量の曲面が、
|
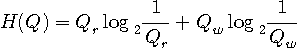
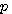 に依存し、こんな簡単なモデルでも少々複雑になります。
に依存し、こんな簡単なモデルでも少々複雑になります。