|
ヒルベルト変換 Hilbert transformation |
|
特定の周波数区間で、信号をそのまま通過させ、それ以外の区間ではカットするような帯域通過フィルターを合成する問題を考えます。 まず、下図のように、ゼロ周波数から上（正のすべての周波数成分）をそのまま通過させ、ゼロ周波数から下（負のすべての周波数成分）をカットするフィルターを考えます。すると、これだけを用いて、任意の帯域通過フィルターを合成することができます。下図のフィルターの周波数特性を
この 信号の複素共役は、周波数領域で言えば、 まず、
です。 実信号を対象にするならば、この複素共役を足して、
を作れば済みます。 次に、
です。 実信号を対象にするならば、この複素共役を足して、
を作ります。
実は、フィルター
ここで、
注１： ヒルベルト変換は 因果律と深い関係にあります。 微分や積分といった線形操作が因果的かどうかという問題は大変基本的なことなので、ディジタル微分器 を参照してください。 更に ＡＲシステム、最小位相推移、 逆システム などが関連するページです。 上の式は、どの正周波数成分も９０度位相を遅らせ、どの負周波数成分も９０度位相を早めるという操作を意味しています。 ヒルベルト変換は線形変換ですから、時間領域表現はコンボリューションで表現できるはずであり、それは下のような形をしています。
ヒルベルト変換のインパルス応答は直角双曲線
右辺の第１項は、
ですが、
となります。 以上から、定数倍は本質的でないので無視すると、上で示したヒルベルト変換の周波数特性（超関数）、
が得られます。 フィルター
アナログ回路では９０度位相差分波器で
この伝達関数から回路定数を決めてRLC回路を設計することができます。 上の伝達関数に微分の周波数特性
すると、
ですから、
上記二つの伝達関数もやはりオールパスですが、その位相特性が入力信号の周波数帯域で（たとえば、
70MHz から 100MHz までの範囲でなど）、できるだけ９０度を保つように
二つの出力の間に９０度位相差特性が実現されているので、それぞれを実部と虚部とみなした複素信号の周波数成分は正だけになります。 実際の９０度位相差分波器では、位相差が相対的に９０度になることに主眼を置いて設計されるため、信号全体がひずむことに留意していません。 すなわち、負周波数のカットを精度よく実現する反面、通過した正周波数成分の位相歪はほったらかしなので、注意を要します。 次に、ディジタルフィルターで実現する問題について考えてみます。 もちろん、上で求めたアナログ伝達関数に、たとえば、積分公式
を代入して
IIR (Infinite Impulse Response)
ディジタルフィルターを実現することもできます。 しかし、この場合はヒルベルト変換を直接的にFIR (Finite Impulse Response) フィルターで近似した方が見通しの良い設計ができ、信号歪のないフィルターを実現できます。 とりあえず、周波数区間
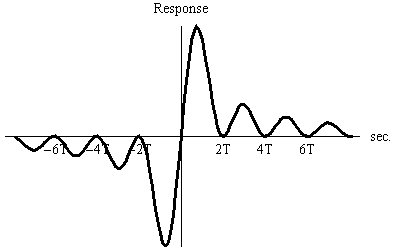
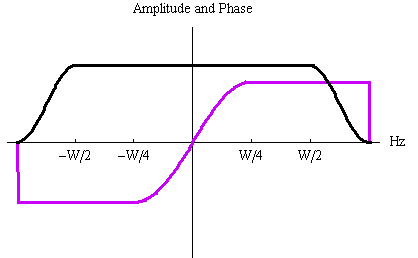
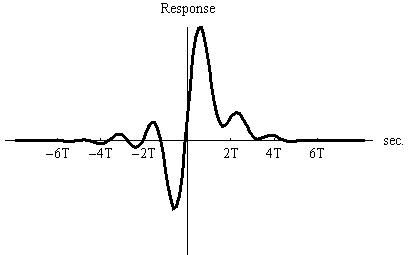
[ -W/2, W/2] Hz について、ヒルベルト変換の周波数特性と時間応答は下図のようになります。 黒い線は振幅、赤い線は位相特性を表しています。 時間応答は振動しながら
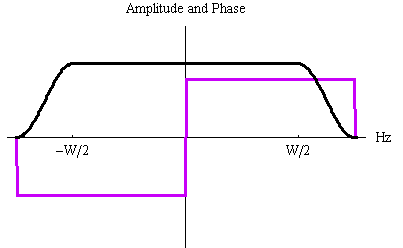
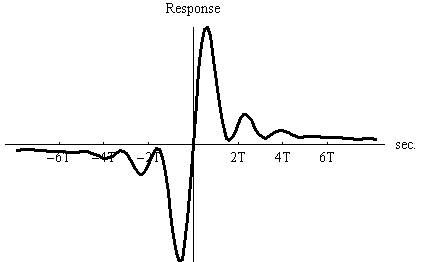
上の応答がなかなか減衰しない理由は、フィルターの帯域を W/2 Hz でいきなりカットしたからなので、今度は W/2 Hz から先でゆるやかに余弦ロールオフをかけてカットしてみます。 ただし、９０度位相特性は厳密に保ったままとします。 すると、下図のように少し速く減衰する時間応答が得られます。
上の周波数特性はまだ周波数ゼロの点で位相の不連続な変化を含んでいます。 しかし、もし対象とする入力信号が直流近辺の成分をあまり含んでいなければ、直流近辺の位相の変化も滑らかにすることができます。 実は、直流成分を強く含んでいる場合でも、VSBAM変調などに適用する場合には矛盾なく目的を果たすことができます（振幅変調を参照）。 下図の例は、区間 [W/4, W/2] Hz の信号に対してヒルベルト変換をする例です。 これらのＦＩＲ
ヒルベルト変換を用いて
注２： 数学的には、ヒルベルト変換に定数
|
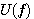とします。
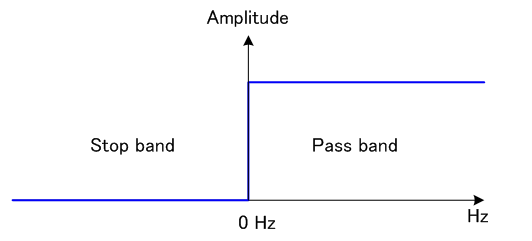
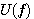をもとに、下記の事実を用いるだけで、任意の帯域通過フィルターを合成することができます。
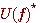は上の青い特性を０ Ｈｚ を中心に折り返したもの、
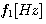以上を通過させ、それ以下（負成分も含めて）をカットするハイパス・フィルターは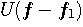
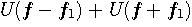
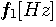
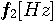までを通過させるバンドパス・フィルターは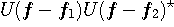
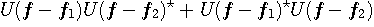
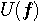は以下のような形をしています。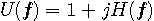
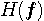はヒルベルト (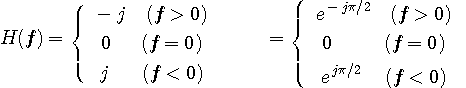 
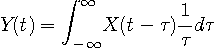
であり、時刻ゼロで特異点をもちます。 ここで、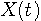
や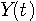 
は複素信号です。 このインパルス応答が前記のようなオールパス９０度位相シフト特性をもつことを確かめてみましょう。 そのために、周波数
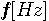の複素トーン信号 
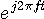にヒルベルト変換を施してみます。
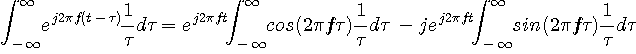(1)
が偶関数で、
が奇関数なので、被積分関数が奇関数となり、ゼロになりそうです。 ただし、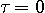
で特異（被積分関数が右から 
に発散し、左からは 
に発散）なので、積分の意味をちゃんと定義しておく必要があります。 一般的な表現は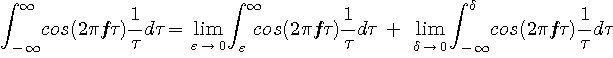
や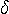 
が独立にゼロに接近すれば積分値はいろいろ変わってしまいます。 この自由度を除くには、同じ速度でゼロに接近させる（
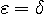とする）のがもっとも典型的ですから、これを仮定すると上の積分はゼロになります。 このような積分結果をコーシー
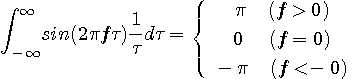
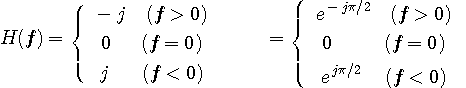
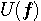を実際に装置化するには、ヒルベルト変換のインパルス応答が時刻ゼロで発散する形をしているので、この問題をクリアしなければなりません。 
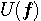を近似実現します。 
の有理関数で与えられます。 ゼロ点
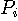や極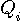 
は一般に複素数です。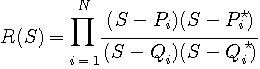
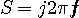
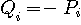としてみます。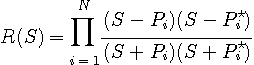
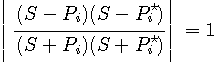
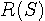はオールパス（すべての周波数成分の大きさを変化させないで通過させる）フィルターになります。 この形のフィルターを二つ用意し、それらを
, 
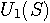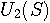であらわします。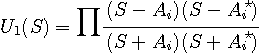
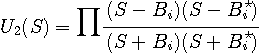
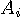と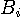 
を最適化します。(100-70) と100 の比を比帯域といっていますが、これが大きくなるにつれて９０度位相差の近似が困難になります。 普通は、高い周波数で変調された信号を対象にしますので、比帯域が非常に小さく、９０度位相差特性が十分な精度で実現できます。 実際の設計手法は回路網の専門書を参考にしてください。 ９０度位相差分波器の構造は下図のようです。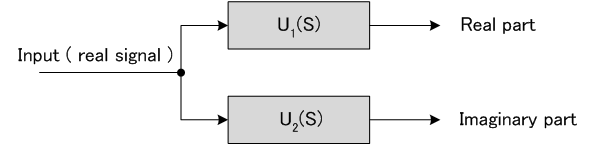
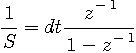前進オイラー ( 
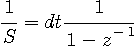後進オイラー公式
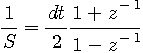台形公式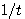 
でゆっくり減衰しています。時間軸に示された目盛りは T=1/W を表しています。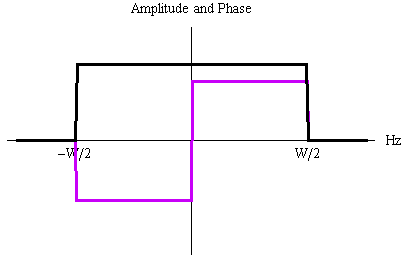
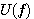を実現するブロック図は下のようになりま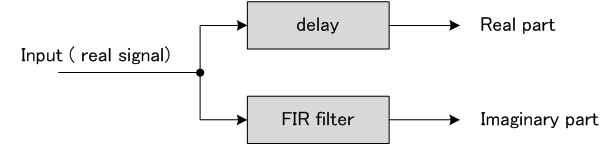す。
を掛けるべきですが、定数はあまり重要ではないので省きました。 また、変数の正負や複素共役の選択によって定義に自由度があり、かつヒルベルト変換のヒルベルト変換は単にマイナス１倍になるので、上のストーリーでは実部と虚部が互いにヒルベルト変換の関係にあるという捉え方で十分です。