

|
微分器 Differential FIR filter |
|
微分(導関数)は
など、いろんな表現があります。 しかし、力学系や電気回路などでは変数が時間なので、因果律 を意識して、
で表現するのが普通ですね。 注1:「物体の速度なんて、所詮は瞬時的な値なんだから、因果律にこだわらんくてもいいじゃん!」と思うかもしれません。 しかし、有限な時間きざみ dt で、信号の微分をタイムラグなしで近似できるかどうかを考えるとき、この概念が重要になってきます。 右辺の差分を遅延作用素
を用いて書くと
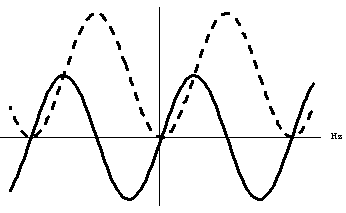
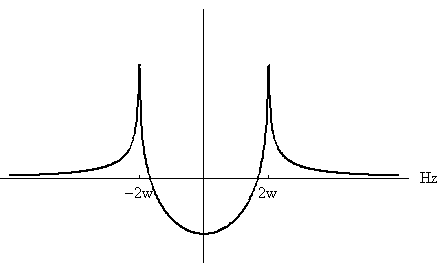
なので、周波数特性は下図のようです。 点線は実部、実線は虚部です。 実部と虚部の間には、たしかに ヒルベルト変換
の関係があります。 これを確かめるには、定数のヒルベルト変換はゼロ、
は反因果的 (anti-causal、未来だけから現在が決まる)で、周波数特性は複素共役になります。 実部と虚部を
なので、 微分の周波数特性は このように、微分特性は周波数に比例して増幅し、無限に広い帯域をもちます。 実際には、無限に広い帯域をもつ信号はないので、有限帯域
[-W/2, W/2] Hz を前提に微分をディジタル信号処理で実現する問題を考えましょう。 AD変換のサンプリング周期を 非因果的FIR: 因果的FIR: 注2: FIR (Finite Impulse Response Digital Filter) は、トランスバーサルタイプの構造をもつフィルターのこと。 <フーリエ展開法>
を単にFIR の長さで打ち切ったにものに一致します。 その理由は、フーリエ級数展開が直交関数展開であるためです。 打ち切りを7次とすれば、FIR
の重み係数
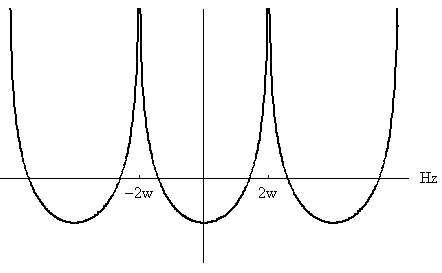
によって得られます。 重み係数の減衰は 1/n であり、7次の打ち切りはかなり無理がありそうです。 このような最適化は、帯域 [-2W, 2W] Hz の全域を占有する信号をも対象にしており、下図に示すように、標本化関数の微分(やはり、1/n のオーダーで減衰)を 1/W 秒周期でサンプルした結果でもあります。 ちなみに、因果的最適解(式(2)の形)を Non-causal FIR filter Causal FIR filter 上のオレンジ色の因果的FIRの周波数特性において、実部は、虚部
をヒルベルト変換した結果(帯域は無限に広がる)
を、周期 4W Hz で移動重畳した結果
の基本周期 [-2W,
2W] Hz を近似しています。 この特性から判断して、帯域全域では正確な微分が実現できないことがいえます。 ただし、実部は直流近辺でフラットなので、実部を底上げする(
<時間領域で最適化>
これを解けば最良解が得られそうです。 ここで、 茶色のスペクトルをもつランダム信号を
として、 <Non-Causal>
<Causal>
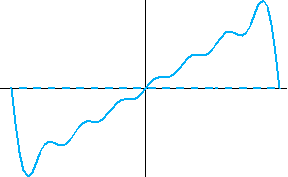
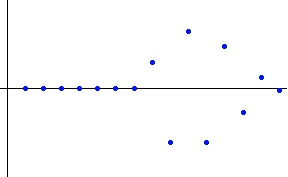
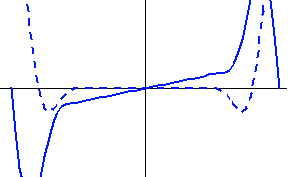
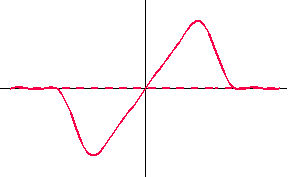
実際に、非因果的FIRを15次、因果的FIRを7次として解いた解と、その周波数特性(点線は実部、実線は虚部)を下に示します。 表示範囲は
[-2W, 2W] Hz です。 いずれも、 Non-causal Causal
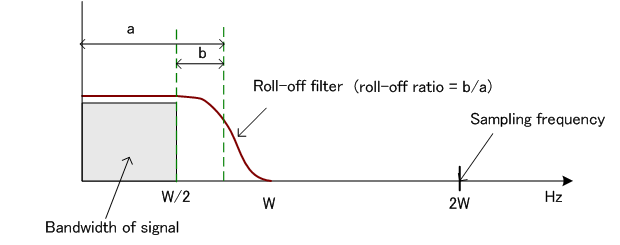
<ロールオフフィルター法>
ですが、このフィルターの応答の微分式を求め、それを 4W sample/sec.でサンプリングして非因果的FIR を求めれば済みます。 この場合の raised cosine ロールオフの応答は、
ですから、この微分式を求めて、 この周波数特性は下のようになり、帯域 [-W, W] Hz
でかなり良い近似を示しています。 ちなみに、片側を単純にカットした因果的FIRの特性はやっぱりフーリエ展開法と同様に、微分特性を満たしません。 ただし、フーリエ展開法と同様、実部がゼロになるように底上げして( Non-causal
Causal
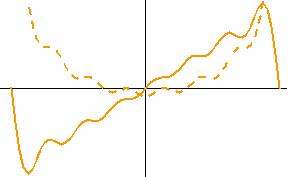
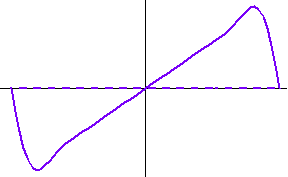
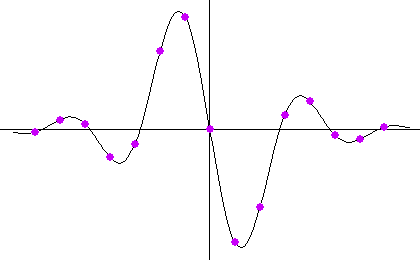
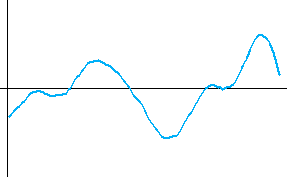
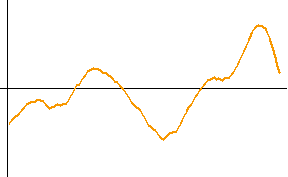
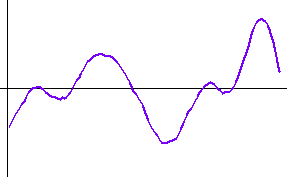
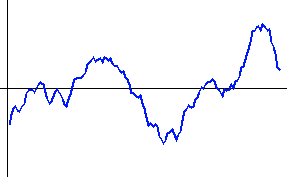
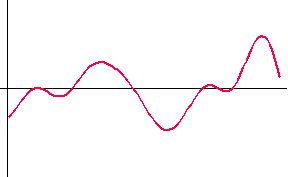
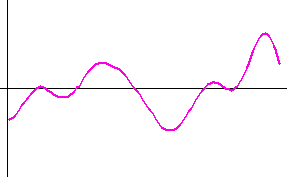
<数値シミュレーション> 最初の黒色のカーブは本当の微分です。 以下、上で用いた色に対応して出力結果を描きます。 本当の微分も、非因果も、因果も、8/(4W) 秒だけ遅延しています。 因果的FIRの前半7タップはゼロなので、これで因果律が満たされていることがいえます。 シミュレーションモデルの入力信号の生成で、帯域制限フィルターの打ち切り誤差が残ったため、高周波雑音が少し残りました。 時間域最適化法の
Causal に大きな雑音が乗っているのは、高域での高い増幅特性が影響したものと思われます。 重要なポイントは、ゼロ交叉時刻(
ideal Fourier series (non-causal) Fourier series (causal) optimum (non-causal) optimum (causal) roll-off filter (non-causal) roll-off filter (causal)
信号の帯域幅よりも速い速度でサンプリングすれば、 上の疑問に対しては否定的です。 因果的FIR のフーリエ展開法において、帯域端におけるフーリエ級数展開は
になってしまい、これは
<積分>
を実現することになります。 右辺第二項は次のように変形されます。
最後の{ }内が非因果的な積分FIRフィルターの係数を表し、
注3: 時間領域最適化法では連立一次方程式を解きますが、自己相関行列の固有値の一部が非常に小さいケースになります。 そのまま"Mathematica"で解かせると帯域外の増幅が極端に大きくなってしまいます。 そこで、自己相関行列の対角項に非常に小さい正数を加算して固有値にほんの少しバイアスをもたせることは帯域外増幅を防ぐために有効です。 その他、直交補空間の処理にはいろんなテクニックがありますが、これらについては最小自乗法や数値計算法の参考書で勉強してください。 注4:複素信号の時間微分については、実部と虚部をそれぞれ時間で微分すれば済みます。 もし、複素信号
を複素信号
が成り立っているので、
すなわち、実部
になります。 |
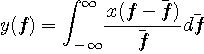
 の様子を調べてみます。
の様子を調べてみます。 
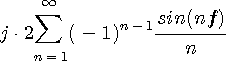
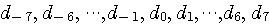 は
は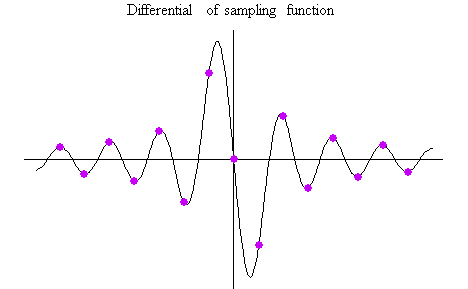
 に近似させると、単に非因果的最適解の片側をカットしたもの (
に近似させると、単に非因果的最適解の片側をカットしたもの (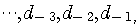 をカット。
をカット。  は残る)になります。 以下に、それぞれの係数と周波数特性(以下、点線は実部、実線は虚部)を図示します。 表示範囲は
[-2W, 2W]Hz です。
は残る)になります。 以下に、それぞれの係数と周波数特性(以下、点線は実部、実線は虚部)を図示します。 表示範囲は
[-2W, 2W]Hz です。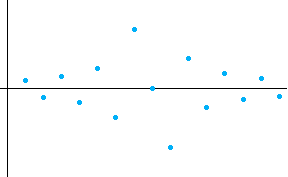
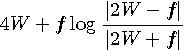
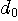 を正の大きな値にして直流近辺の実部をゼロにする)ことによって、狭帯域信号の微分に適用できそうです。 裏を返せば、サンプリング速度をどんどん上げて直流成分を調整すれば、因果的FIRで微分を近似できるということです。 上のオレンジ色の実部は底上げした結果です。 フーリエ展開法は
を正の大きな値にして直流近辺の実部をゼロにする)ことによって、狭帯域信号の微分に適用できそうです。 裏を返せば、サンプリング速度をどんどん上げて直流成分を調整すれば、因果的FIRで微分を近似できるということです。 上のオレンジ色の実部は底上げした結果です。 フーリエ展開法は
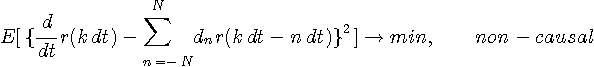
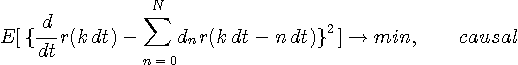
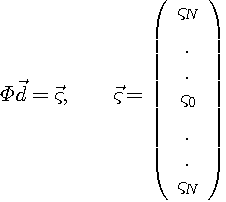
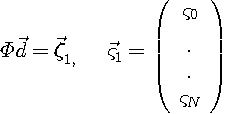
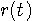 の通過帯域 [-W, W] Hz で微分特性
の通過帯域 [-W, W] Hz で微分特性  を実現しています。 ただし、因果的微分の帯域外の増幅はかなり大きくなります。
を実現しています。 ただし、因果的微分の帯域外の増幅はかなり大きくなります。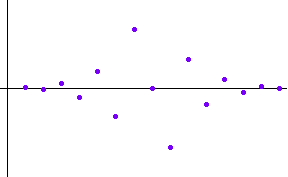
 とすると、ロールオフフィルターの帯域は
とすると、ロールオフフィルターの帯域は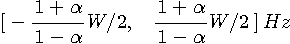
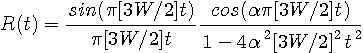
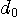 を適当に調節して)あります。
を適当に調節して)あります。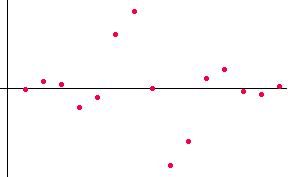
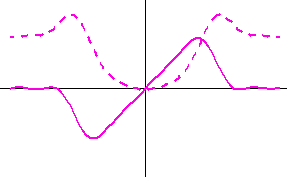
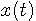 をアナログ・トランスバーサルフィルターに入力して、本当の微分結果と比較してみます。 タップ間隔は
1/(4W) 秒です。
をアナログ・トランスバーサルフィルターに入力して、本当の微分結果と比較してみます。 タップ間隔は
1/(4W) 秒です。 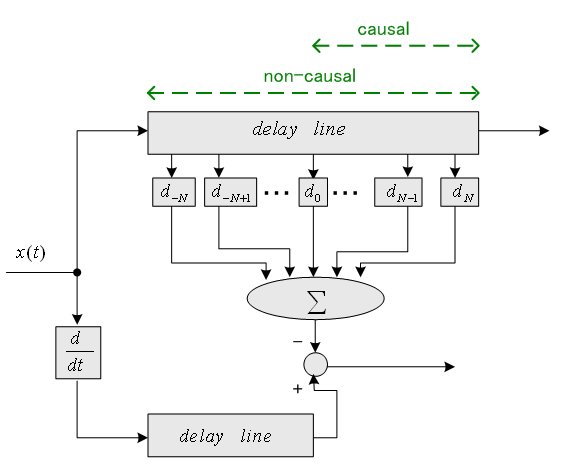
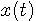 の極大と極小の時刻)が正確かどうかですが、フーリエ展開法以外では理想微分と正確に一致しています。 最適解は、Mathematica
の連立一次方程式を単純に適用しただけなので、高域を抑える工夫はいろいろあります。 7次の打ち切りでは厳しいかもしれないが、次数を上げれば、そえれぞれ精度が上がりそうです。
の極大と極小の時刻)が正確かどうかですが、フーリエ展開法以外では理想微分と正確に一致しています。 最適解は、Mathematica
の連立一次方程式を単純に適用しただけなので、高域を抑える工夫はいろいろあります。 7次の打ち切りでは厳しいかもしれないが、次数を上げれば、そえれぞれ精度が上がりそうです。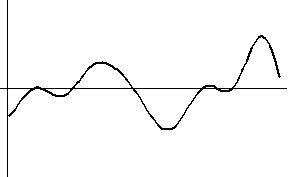
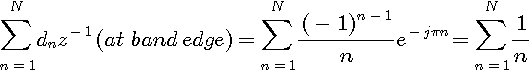
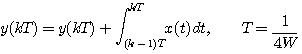
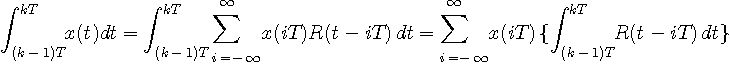
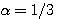 として下図のようになります。 因果的積分器の設計は、上の微分器の設計に沿って進めることができます。
として下図のようになります。 因果的積分器の設計は、上の微分器の設計に沿って進めることができます。 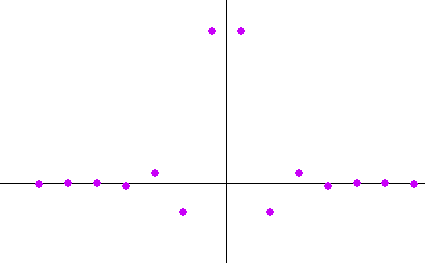
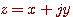 の複素関数
の複素関数 で微分したい場合は、微分可能ならば、コーシー・リーマン (
で微分したい場合は、微分可能ならば、コーシー・リーマン (  だけで偏微分してよいことになります。 複素信号の実関数は、評価関数として信号処理などで頻繁に登場しますが、これを
だけで偏微分してよいことになります。 複素信号の実関数は、評価関数として信号処理などで頻繁に登場しますが、これを
 とすると、単に
とすると、単に  と
と  の実関数なので、これを複素信号
の実関数なので、これを複素信号  で微分することは、
で微分することは、 と
と  で微分して複素信号を再構成することを意味します。 したがって、このときの微分は
で微分して複素信号を再構成することを意味します。 したがって、このときの微分は