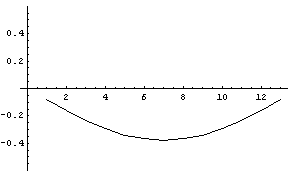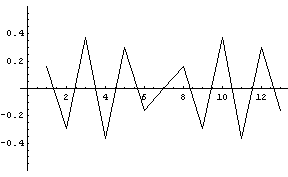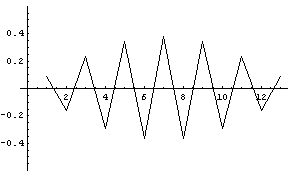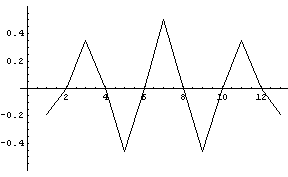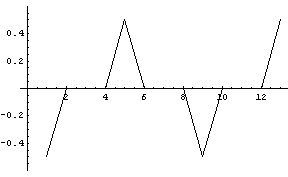|
自己相関行列 Auto-correlation matrix |
|
説明の簡単のため、実信号を扱います。 定常確率過程の自己相関
を次のように配列し、これを自己相関行列といいます。
これは、対称行列であり、またToeplitz 行列(斜めに同じ要素が並ぶ行列)です (Otto Toeplitz, 1881-1940)。 対称行列なので、固有値はすべて実数です。 また、固有ベクトルも実数になります。 以下に、自己相関行列の固有値に関する重要な性質を挙げます。
(1) 自己相関行列の固有値はすべて非負(ほとんどのケースですべて正)。 すべての小行列 この意味は、行列式の値がすべての固有値の積で与えられることから、帰納法を念頭に置けば理解できると思います。 この判定に持ち込むために、行列式をブロック行列に分解して計算する次のような公式を導入します。
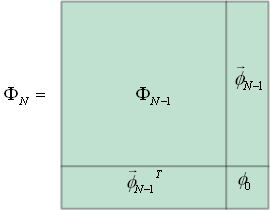
特別な場合として、r = N-1 として自己相関行列に適用すると、
ここで、上の公式からベクトル
が得られます。 したがって、もし、右辺の( )内が常に非負ならば、
なので、Sylvester の判定を満たします。 実際、
(2) Nが大きいとき、固有値は近似的に電力スペクトルを与える。
すなわち、
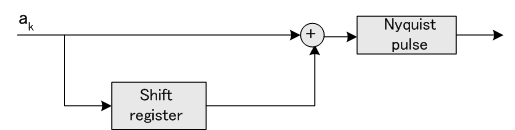
ということになります。 ただし、正方行列による打ち切りを伴うので、厳密にコンボリューションとはいえませんが・・・。 この解釈によれば、信号 <Duo-binary>
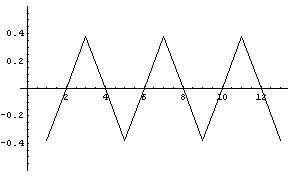
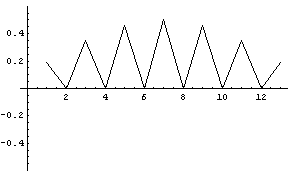
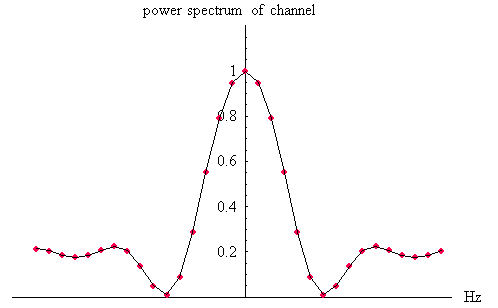
で表されます。 ここでは、パルスを標本化関数(0%ロールオフ)とします。 このとき、信号の振幅スペクトルは Raised Cosine であり、直流が最大で、周波数とともに減少し、ナイキスト周波数(シンボルのクロック周波数)でゼロになります。
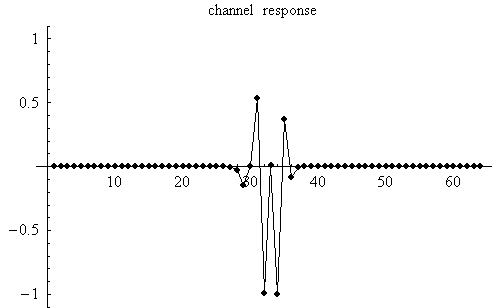
この信号をシンボルに同期したタイミングでサンプルした離散信号の自己相関は、
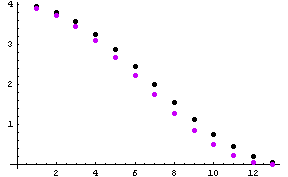
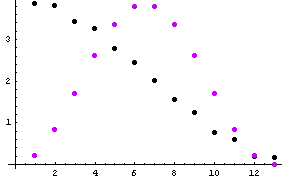
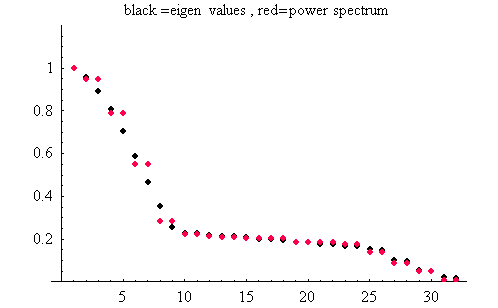
のようになります。 これから 13次の自己相関行列を作り、固有値を求めると、下図のようにプロットされます。 黒が固有値、赤はduo-binary 信号の電力スペクトルです。 かなり良く一致していることがわかります。
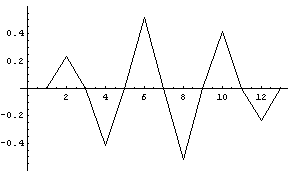
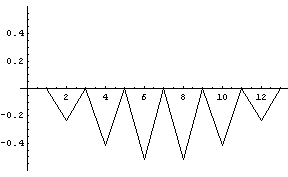
固有値の大きい方から順番を振って、1番、2番、7番、13番、14番の固有値に対応する固有ベクトルを下に示します。 ほぼ、該当する周波数成分を強く含んでいることがわかります。
<Class-4 Partial response>
です。 特に、n=1 をクラス4・パーシャルレスポンスといい、振幅スペクトルは直流とナイキスト周波数でゼロとなるオフセット余弦の形をしています。 直流成分を含まないので、直流を記録しないディジタル磁気録音などに広く応用されています。 自己相関は
のようになり、13次の自己相関行列の固有値をプロットすると下図のようになります。
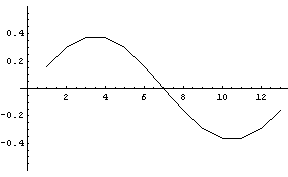
一見、固有値と電力スペクトルが一致していないようですが、固有値は大きい順に求まるので、下の固有ベクトルを見て、周波数の順番に並べかえる必要があります。 そうすれば、赤のスペクトルに近似していることが認められるはずです。 上と同様に、固有値の大きい順に、1番、2番、7番、12番、13番に対応する固有ベクトルを下に示します。
注1:duo-binaryの固有ベクトルを用いてclass-4の信号を固有値分析しても、class-4の電力スペクトルを与えません。 3. 固有ベクトルによる信号分析の例
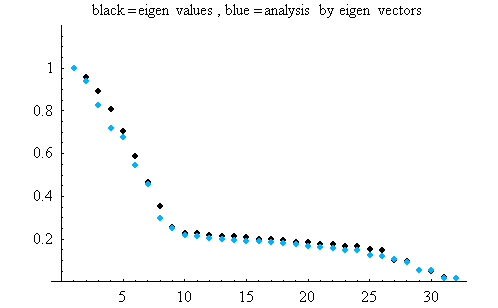
受信信号の自己相関行列の固有値は大きなものから求まるので、上の電力スペクトルも大きさの順に並べ替えて表示すると次のようにほぼ一致しています。
次に、長いランダムデータを送信したときの受信信号を、固有ベクトルをタップ重みとするFIRフィルターに通し、その出力の平均電力を求めると下図の青色のようになり、固有値に一致することが分かります。
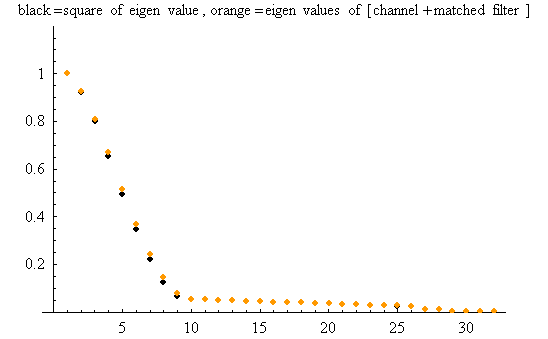
通信では受信信号を整合フィルターに通すことが広く行われます。 このとき、整合フィルターの振幅特性とチャンネルの振幅特性は同じなので、整合フィルターの出力信号に対して上と同様の直交分析を行うと、固有値の二乗が得られるはずです。実際、シミュレーションした結果は下図のように一致しました。
|
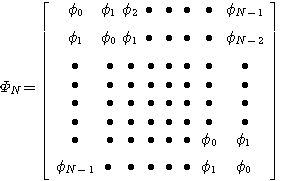
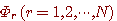 の行列式が非負 <==> すべての固有値は非負
の行列式が非負 <==> すべての固有値は非負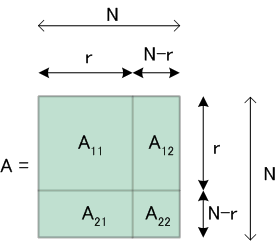
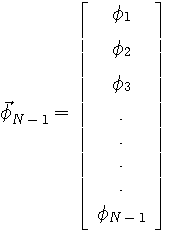
 がフィルター(
がフィルター(