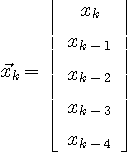|
ARモデル Auto-regressive model |
|
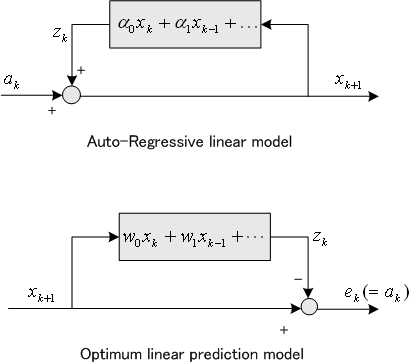
日本語で、自己回帰モデルと呼んでいます。今日までの我が身の生き方から明日の我が身を占うという、因果律に従うモデルです。経済指標予測、気象予測、河川流量予測などの複雑な非物理系(システムの細部を厳密に記述できないシステム)のモデルとして、広く使われています。一般的に次のように書けます。
線形ARモデルの場合、その逆は線形予測モデルになります。
実際、線形ARモデル
に対して、順次
が得られ、自己相関行列が正則なので解は一意であり、最適予測は
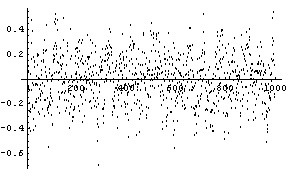
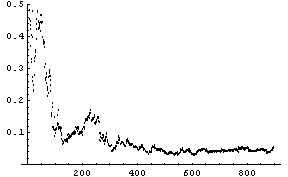
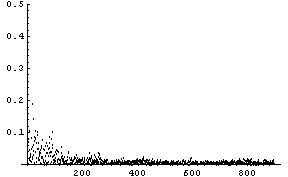
を満たすことがいえます。 そして、このことから次がいえます。 線形予測は擾乱 このことをシミュレーションで実証してみましょう。 ARモデルを
として、最急降下法
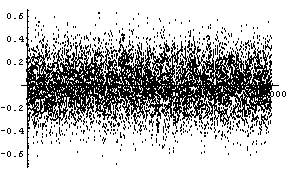
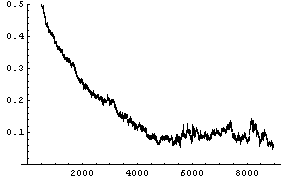
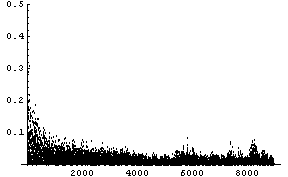
を実行します。 期待される結果が
横軸は修正回数であり、10000回の修正を実行していますが、
注1: ARモデルは明らかに因果的です。 そのモデルが安定ならば、逆はいつも存在します。 このような線形システム(因果的で、因果的逆が存在する場合)を最小位相推移といっています。 詳しくは、 因果律、 最小位相推移、 逆システムを参照してください。 注2:ARモデルは最小位相推移システムの特別な場合です。 最小位相推移ならばブラインド等化はいつも予測システムで簡単に実現可能です。 ブラインド問題の困難さは非最小位相推移の場合に生じます。 工学的応用では、ほとんんどのケースが非最小位相推移です。 |
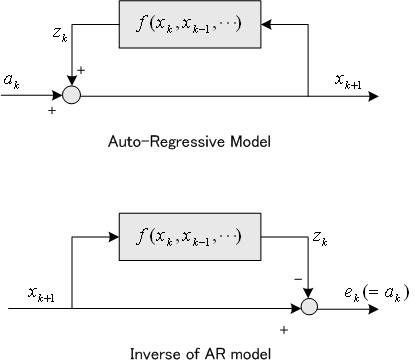
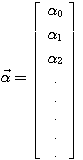
 を参照しないで
を参照しないで